DP
두번 이상 반복 계산되는 부분 문제들의 답을 미리 저장(메모이제이션)해 한번만 계산 되도록 함으로써 속도의 향상을 꾀하는 방식의 알고리즘 패러다임
이항 계수를 계산하는 함수 bino(n,r)를 완전 탐색 방식으로 작성하면 아래와 같이 중복되는 부분 문제가 발생한다. 이때 DP를 적용하면 부분 문제를 중복 계산하지 않아 성능을 높일 수 있다. 중복되는 부분 문제가 많을수록 성능은 더욱 높아진다.
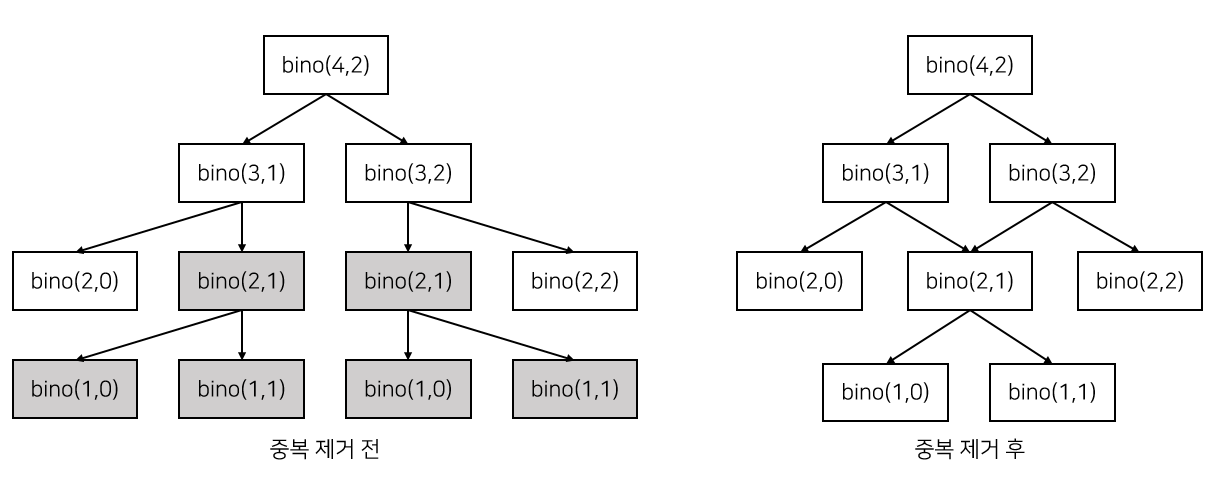
[동작 방식]
- 주어진 문제를 완전 탐색을 이용해 해결한다.
- 중복된 부분 문제를 한번만 계산하도록 메모이제이션을 적용한다.
최적화 문제와 DP
최적화 문제란 문제의 답이 하나가 아닌 여러개 이고 그 중 어떤 기준에 따라 가장 좋은 답을 찾아 내는 문제를 말한다. 예를 들어 n개의 사과 중에서 r개를 골라 무게의 합을 최대화하는 문제, 또는 가장 무거운 사과와 가장 가벼운 사과의 무게 차이를 최소화하는 문제 등이 최적화 문제이다. 최적화 문제를 푸는 가장 기본적인 방법은 완전 탐색이다. 모든 답을 생성해 보고 그 중 가장 좋은 것을 찾아내면 되기 때문이다.
그런데 최적화 문제가 최적 부분 구조(optimal substructure)를 만족한다면 DP를 사용해 더 효율적으로 풀 수 있다. 최적 부분 구조란 각 부분 문제의 최적해로 전체 문제의 최적해를 풀 수 있다는 조건을 말한다. 즉 지금까지의 선택과 상관없이 각 부분 문제를 최적으로 풀면 전체 문제의 최적해를 구할 수 있다. 따라서 각 부분 문제의 최적해를 메모이제이션 한다면 최적화 문제를 효율적으로 풀 수 있게 된다.
대표적으로 서울에서 부산까지 가는 최단 경로 문제가 최적 부분 구조를 만족한다. 서울에서 부산까지 가는 최단 경로를 (서울, 대전), (대전, 부산)으로 나누고 두 구간의 최단 경로를 찾아서 둘을 이으면 서울에서 부산까지 가는 최단 경로를 얻을 수 있다. 즉 각 부분 문제의 최적해인 (서울,대전)의 최단 경로와 (대전, 부산)의 최단 경로로 전체 문제의 최적해인 (서울,부산)의 최단 경로를 얻을 수 있기에 최적 부분 구조를 만족한다. 반면에 고속도로의 통행료 합이 3만원이 넘지 않는 서울에서 부산까지의 최단 경로 문제는 최적 부분 구조를 만족하지 않는다. 서울에서 부산까지 가는 최단 경로를 (서울, 대전), (대전, 부산)으로 나누면 (대전, 부산)의 최단 경로는 (서울, 대전)의 최단 경로 통행료에 따라 결정된다. 따라서 부분 문제의 최적해가 전체 문제의 최적해로 이어지지 않는다.
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘 패러다임 - 4] 분할 정복 (0) | 2022.10.21 |
|---|---|
| [알고리즘 패러다임 - 3] Greedy (0) | 2022.10.05 |
| [알고리즘 패러다임 - 1] Brute Force (0) | 2022.10.04 |
| 순열, 조합 - Brute Force (1) | 2022.10.03 |
| 이진 탐색 (0) | 2022.09.16 |
