서론
B Tree와 B+ Tree는 이진 탐색 트리를 확장해 하나의 노드가 2개 이상의 자식을 가질 수 있게 만든 트리이며 주로 데이터베이스, 파일 시스템에서 사용된다.
하드 디스크는 블록 단위로 읽기/쓰기 작업을 수행한다. DB의 모든 행은 블록에 저장된다. 만약 특정 행을 조회하는 쿼리를 수행하려면 행이 저장된 모든 블록을 모두 탐색해야하는데 이는 비효율적이다. 그래서 인덱스를 사용한다. 행의 키를 키로, 블록 주소를 값으로 갖는 인덱스를 사용한다. 인덱스가 저장된 블록 + 1개의 행이 저장된 블록만 탐색하면 되므로 탐색할 블록 개수가 줄어든다.
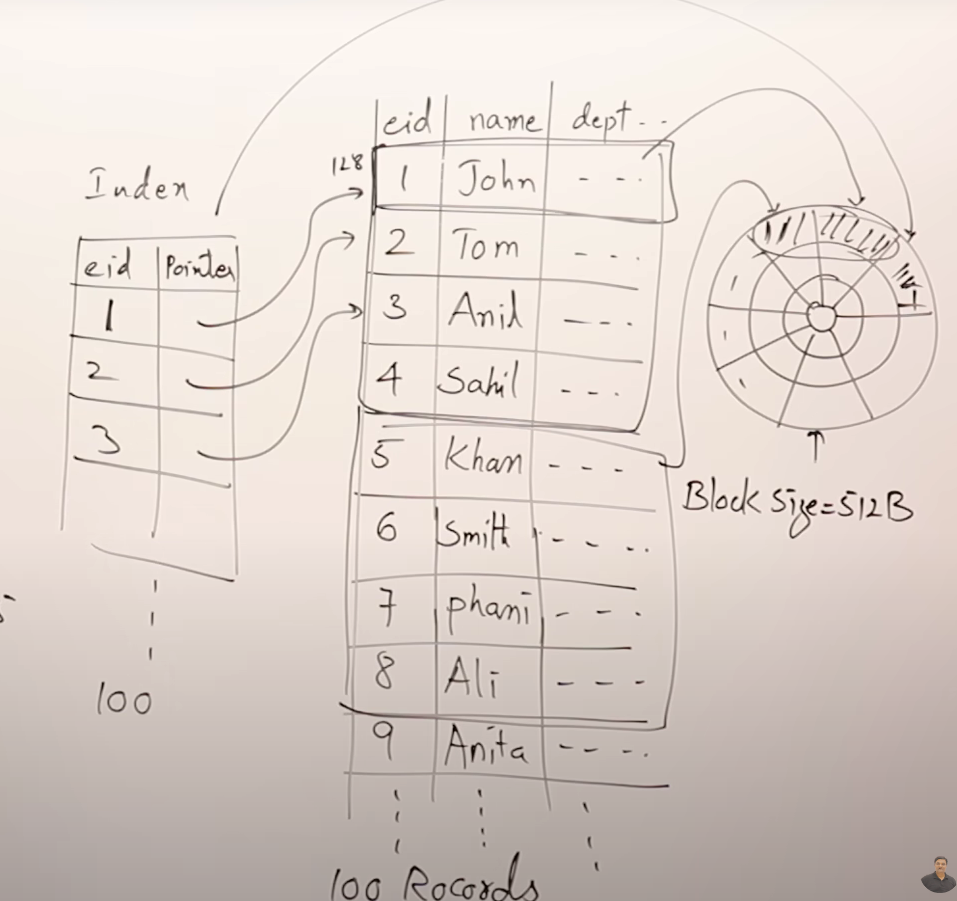
인덱스를 위한 인덱스
행이 많아지면 인덱스 블록 개수도 증가한다. 때문에 인덱스를 위한 인덱스(high level index)를 둔다.
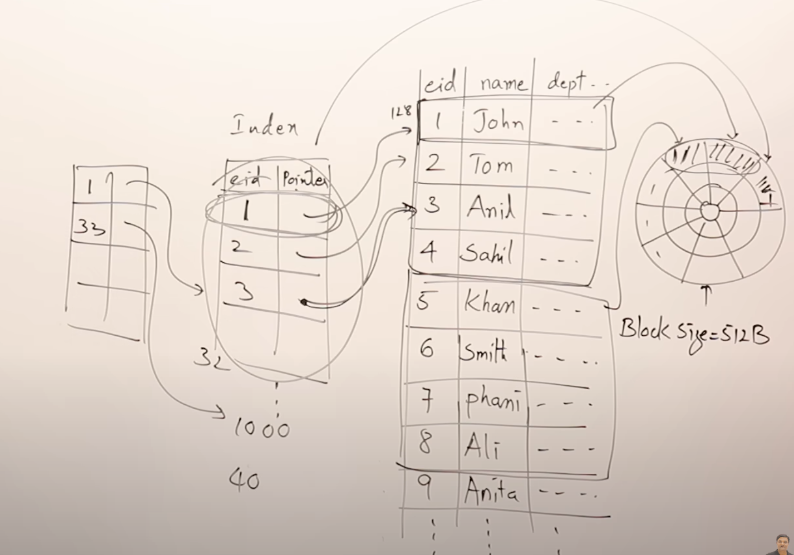
DB 행이 증가할수록 인덱스를 계속 만들 것이고, 결국 인덱스들은 트리 구조를 형성하며 탐색할 블록 개수는 줄어든다. 때문에 DB 또는 파일 시스템이 인덱스 저장 용도로 트리를 사용한다.
M-Way Search Tree
위 트리를 M-Way Search Tree로 표현할 수 있다. M-Way Search Tree란 한 노드가 M개의 자식을 가지며 M-1개의 키를 갖는 탐색 트리를 말한다. BST가 2-Way Search Tree이다.
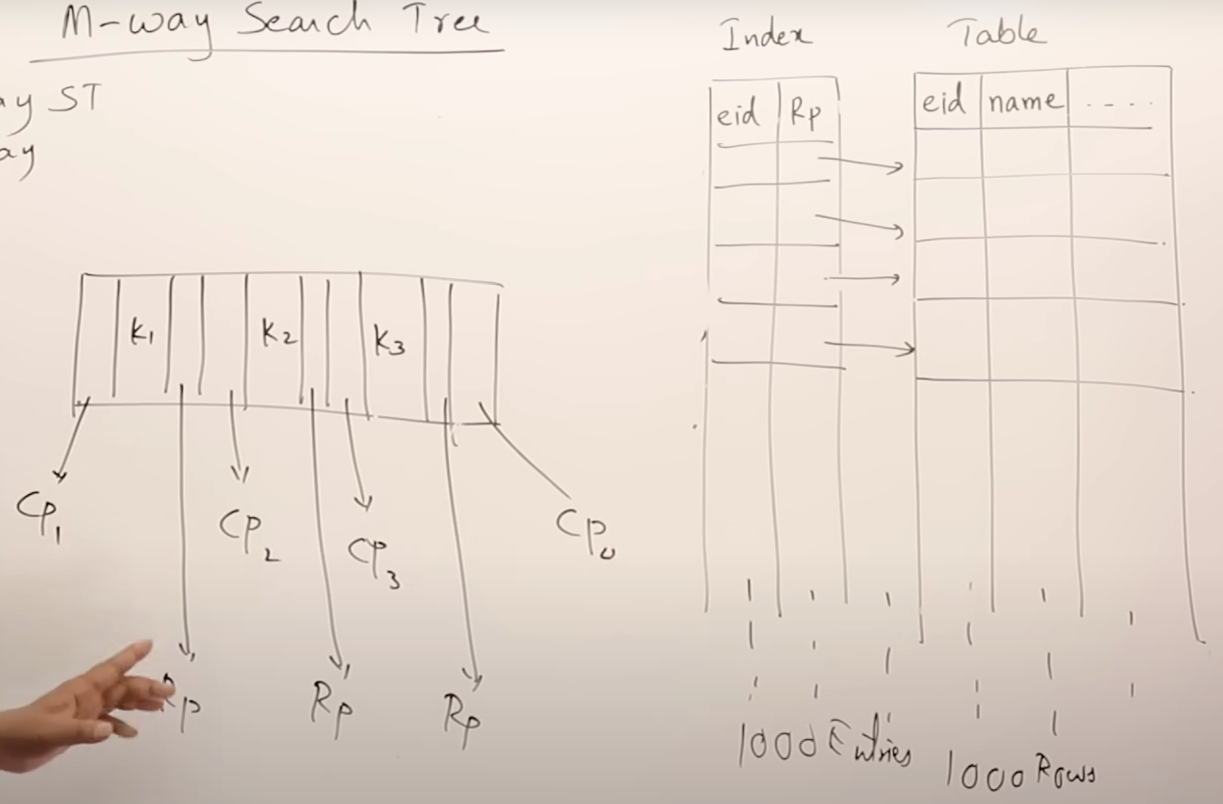
탐색 트리의 중요한 점은 균형을 유지해야한다. 균형이 깨질 경우 최악의 경우 시간 복잡도가 매우 증가한다. 때문에 스스로 균형을 맞추는 B 트리, B+ 트리를 사용한다.
B 트리, B+ 트리
B 트리 특징
- 노드의 키들은 항상 정렬됨
- 내부 노드는 ceil(M/2) ~ M개의 자식을 가져야만 하며, 최대 M개의 자식을 가질 수 있는 B 트리를 M차 B 트리라고 함
- 모든 리프 노드들은 같은 레벨에 존재
B 트리의 모든 노드는 키에 해당하는 DB 행이 저장된 블록 주소(RP)를 가지고 있다.
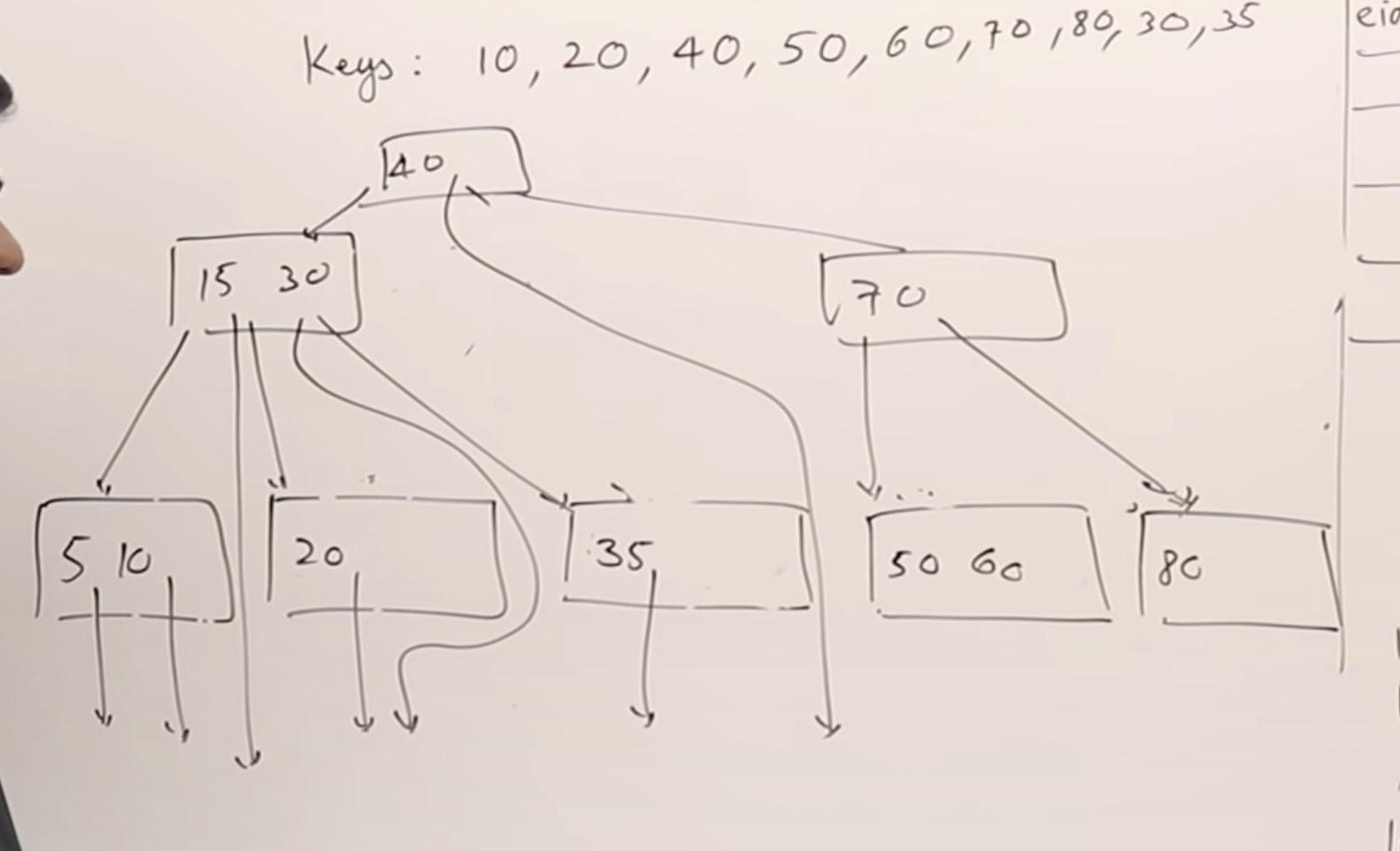
B+ 트리 특징
- B+ 트리는 오직 리프 노드에서만 레코드 포인터를 가짐, 대신 리프 노드에 모든 키들이 존재
- 모든 리프노드는 연결리스트처럼 연결됨
리프 노드까지 내려가야만 탐색이 완료된다는 단점이 있지만, 범위 탐색을 빠르게 할 수 있다는 장점이 있다.

'Computer Science > DataStructure' 카테고리의 다른 글
| Hash (0) | 2024.07.29 |
|---|---|
| Heap (0) | 2024.07.24 |
| Segment Tree (0) | 2023.10.08 |
| Binary Search Tree (0) | 2023.09.11 |
| Tree (0) | 2023.09.06 |
