LinkedList
LinkedList는 리스트의 한 종류이다. 노드들이 물리적인 메모리 주소상으로 연속되어 있지 않지만 노드가 다음 노드로 갈 수 있는 포인터를 가짐으로써 노드들이 논리적으로 연속되어 있다.
연결 리스트에서 하나의 원소를 노드라고 한다. 노드는 데이터 필드와 링크 필드로 나뉘는데 데이터 필드는 리스트에 저장될 원소의 값을 저장하며 링크 필드는 다음 노드의 참조값을 저장한다.
연결리스트의 가장 큰 장점은 원소의 삽입, 삭제의 시간복잡도가 O(1)이다. 때문에 원소의 삽입, 삭제가 빈번하면 연결 리스트 사용을 고려할만하다. 단점은 특정 위치의 원소를 찾아가는 시간 복잡도가 O(N)이다. 배열(배열 기반 리스트)와 달리 랜덤 엑세스가 안되기 때문이다.
연결 리스트의 종류
연결 리스트는 총 세 종류로 나뉜다.
1. 단순 연결 리스트
단방향 링크 구조를 가진다. 노드의 링크 필드는 하나이며 다음 노드의 주소를 가진다. 단순 연결 리스트에서 마지막 노드의 링크 필드는 NULL이기 때문에, 링크 필드가 NULL인 노드가 마지막 노드임을 알 수 있다. 단방향 링크 구조이므로 다음 노드에서 이전 노드로 이동할 수 없다.

2. 이중 연결 리스트
양방향 링크 구조를 가진다. 노드의 링크 필드는 두개이며 이전 노드와 다음 노드의 주소를 가진다. 이중 연결 리스트에서 첫 번째 노드의 이전 링크 필드는 NULL이며, 마지막 노드의 다음 링크 필드는 NULL이다. 양방향 링크 구조이기에 다음 노드에서 이전 노드로 이동할 수 있다.

3. 원형 연결 리스트
원형 연결 리스트는 링크가 원형으로 연결되는 구조이다. 단순 원형 연결 리스트와 이중 원형 연결 리스트로 구분된다. 아래는 단순 원형 연결 리스트의 구조이다. 마지막 노드의 다음 링크 필드는 첫 번째 노드의 주소를 가진다.

아래는 이중 원형 연결 리스트의 구조이다. 마지막 노드의 다음 링크 필드는 첫 번째 노드의 주소를 가지며 첫 번째 노드의 이전 링크 필드는 마지막 노드의 주소를 가진다.
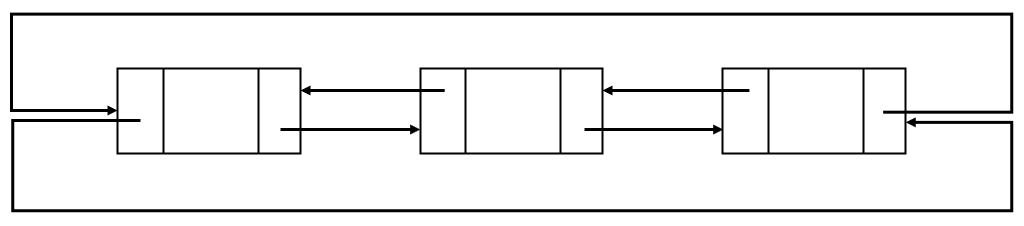
리스트가 순환, 원형 구조일경우 원형 연결 리스트로 구현한다.
Head, Tail
Head 포인터란 연결 리스트의 첫 번째 노드를 가리키는 포인터이다. Head 포인터만 가지고 있으면 리스트를 완전 탐색할 수 있다. 따라서 Head 포인터만 가지고 있으면 리스트를 가지고 있는 것이다. 또한 설계에 따라 Tail 포인터를 둘 수 있다. Tail 포인터는 연결 리스트의 마지막 노드를 가리키는 포인터이다.
보통 단순 연결 리스트는 Head 포인터만 가지며 이중 연결 리스트는 Head와 Tail 포인터를 가진다. 이중 연결 리스트가 양 끝단의 포인터를 가지는 이유는 양 끝단의 노드 삽입, 삭제가 O(1)이 되며, 양 끝단에서부터의 탐색이 용이하다. 이를 통해 특정 인덱스의 노드로 찾아가는 시간 복잡도를 N번에서 N/2번으로 줄일 수 있다. 리스트를 반으로 나누고 특정 노드가 중간보다 앞에 있으면 head 포인터를, 중간보다 뒤에 있다면 tail 포인터를 통해 탐색한다.
리스트가 순환, 원형 구조일 경우 원형 연결 리스트로 구현한다. 시작 노드에서 탐색해 다시 시작 노드로 되돌아 올 수 있으며 임의의 노드 위치에서 한 방향으로 리스트를 완전 탐색 할 수 있다. 주의할 점은 순환 구조이기에 무한 루프에 빠지지 않도록 주의해야한다.
단순 연결 리스트 구현
연결 리스트의 핵심 연산은 두 가지이다. 새 노드를 연결리스트의 노드와 연결하는 연산(link), 노드의 연결을 끊는 연산(unlink)이다.
단순 연결 리스트의 노드는 값을 저장하는 value와 다음 노드의 포인터를 저장하는 next 필드를 갖으며, head 포인터가 리스트의 맨 앞단을 가리키고 있다. 단순 연결 리스트의 경우 link, unlink 연산을 두 경우로 구분할 수 있다.
1. 맨 앞단에 노드 삽입, 삭제
void linkFirst(int value) {
Node newNode = new Node(value);
newNode.next = head;
head = newNode;
}
int unlinkFirst() {
int vaule = head.value;
head = head.next;
return value;
}2. 중간 또는 끝단에 노드 삽입, 삭제
//succ 노드 뒤에 새 노드 삽입
void linkAfter(Node succ, int value) {
Node newNode = new Node(value)
newNode.next = prev.next;
prev.next = newNode
}
//succ 노드의 다음 노드 삭제
int unlinkAfter(Node succ) {
int x = succ.next.value;
succ.next = succ.next.next;
return x;
}만약 맨 앞단을 더미 노드로 고정시킨다면 맨 앞단에 노드 삽입, 삭제 코드를 넣어줄 필요가 없다. 리스트 맨 앞에는 무조건 더미 노드가 있기에 리스트 중간 또는 끝단에만 노드 삽입, 삭제가 일어나기 때문이다. 그래서 구현이 더 쉽지만 더미 노드만큼 메모리 낭비가 발생한다. 노드의 메모리 크기가 크다면 더미 노드를 사용하지 않는 것이 좋다.
아래는 더미 노드로 구현한 단순 연결 리스트이다. 더미 노드를 쓰기 때문에 맨 앞단에 노드 추가, 삭제 연산을 구현할 필요가 없다.
public class SinglyLinkedList implements List {
static private class Node {
int value;
Node next;
Node(int value, Node next) {
this.value = value;
this.next = next;
}
}
private Node head;
private int size;
public SinglyLinkedList() {
//더미노드 생성
//head에서 x번 이동 = 인덱스 x-1번 노드
head = new Node(0, null);
size = 0;
}
private void rangeCheck(int index) {
if (index < 0 || index >= size) throw new IndexOutOfBoundsException();
}
//succ 노드 뒤에 새 노드 삽입
private void linkAfter(Node succ, int value) {
Node newNode = new Node(value, succ.next);
succ.next = newNode;
size++;
}
//succ 노드의 다음 노드 삭제
private int unlinkAfter(Node succ) {
int x = succ.next.value;
succ.next = succ.next.next;
size--;
return x;
}
//index 위치 노드 반환
private Node Node(int index) {
Node cur = head;
for(int i=0; i<index + 1; i++) cur = cur.next;
return cur;
}
@Override
public boolean add(int value) {
linkAfter(Node(size-1), value);
return true;
}
@Override
public void add(int index, int value) {
if(index == size) {
linkAfter(Node(size-1), value);
return;
}
rangeCheck(index);
linkAfter(Node(index-1), value);
}
@Override
public int remove(int index) {
rangeCheck(index);
return unlinkAfter(Node(index-1));
}
@Override
public boolean remove(Integer value) {
int index = indexOf(value);
if(index == -1) return false;
unlinkAfter(Node(index-1));
return true;
}
@Override
public int get(int index) {
rangeCheck(index);
return Node(index).value;
}
@Override
public void set(int index, int value) {
rangeCheck(index);
Node(index).value = value;
}
@Override
public boolean contains(int value) {
if(indexOf(value) == -1) return false;
return true;
}
@Override
public int indexOf(int value) {
Node cur = head;
for(int i=0; i<size; i++) {
cur = cur.next;
if(cur.value == value) return i;
}
return -1;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return (size == 0);
}
@Override
public void clear() {
head.next = null;
size = 0;
}
public void print(){
System.out.println("--------");
Node node = head;
for(int i=0; i<size; i++){
node = node.next;
System.out.println(node.value + " ");
}
System.out.println("--------");
System.out.println();
}
}이중 연결 리스트 구현
이중 연결 리스트의 노드는 값을 저장하는 value와 다음 노드의 포인터를 저장하는 next 필드, 이전 노드의 포인터를 저장하는 prev 필드를 갖는다. 그리고 head 포인터가 리스트의 맨 앞단을 가리키며, tail 포인터가 리스트의 맨 뒷단을 가리킨다. 이중 연결 리스트의 경우 link, unlink 연산을 세 경우로 구분할 수 있다.
1. 맨 앞단에 노드 삽입, 삭제
private void linkFirst(int value) {
Node h = head;
Node newNode = new Node(null, value, h);
head = newNode;
if(h == null)
tail = newNode;
else
h.prev = newNode;
size++;
}private int unlinkFirst() {
int value = head.value;
Node next = head.next;
head = next;
if(next == null)
tail = null;
else
next.prev = null;
size--;
return value;
}2. 맨 뒷단에 노드 삽입, 삭제
private void linkLast(int value) {
Node t = tail;
Node newNode = new Node(t, value, null);
tail = newNode;
if(t == null)
head = newNode;
else
t.next = newNode;
size++;
}private int unlinkLast() {
int value = tail.value;
Node prev = tail.prev;
tail = prev;
if(prev == null)
head = null;
else
prev.next = null;
size--;
return value;
}3. 중간에 노드 삽입, 삭제
//succ 노드 앞에 노드 삽입
private void linkBefore(int value, Node succ) {
if(succ == head) {
linkFirst(value);
return;
}
Node newNode = new Node(succ.prev, value, succ);
succ.prev.next = newNode;
succ.prev = newNode;
size++;
}//노드 삭제
private int unlink(Node x) {
if(x == head) {
return unlinkFirst();
}
else if(x == tail) {
return unlinkLast();
}
//중간 노드 삭제
int value = x.value;
x.prev.next = x.next;
x.next.prev = x.prev;
size--;
return value;
}만약 맨 앞단과 뒷단을 더미 노드로 고정시킨다면 맨 앞단에 노드 삽입, 삭제 코드와 맨 뒷단에 노드 삽입, 삭제 코드를 넣어줄 필요가 없다. 리스트 맨 앞과 맨 뒤에는 무조건 더미 노드가 있기에 리스트 중간에만 노드 삽입, 삭제가 일어나기 때문이다. 그래서 구현이 더 쉬워진다.
아래는 더미 노드를 쓰지 않은 이중 연결 리스트의 구현이다.
public class DoublyLinkedList implements List {
static private class Node {
int value;
Node prev;
Node next;
Node(Node prev, int value, Node next) {
this.prev = prev;
this.value = value;
this.next = next;
}
}
private Node head;
private Node tail;
private int size;
private void rangeCheck(int index) {
if (index < 0 || index >= size) throw new IndexOutOfBoundsException();
}
//맨 앞단에 노드 삽입
private void linkFirst(int value) {
Node h = head;
Node newNode = new Node(null, value, h);
head = newNode;
if(h == null)
tail = newNode;
else
h.prev = newNode;
size++;
}
//맨 뒷단에 노드 삽입
private void linkLast(int value) {
Node t = tail;
Node newNode = new Node(t, value, null);
tail = newNode;
if(t == null)
head = newNode;
else
t.next = newNode;
size++;
}
//맨 앞단의 노드 삭제
private int unlinkFirst() {
int value = head.value;
Node next = head.next;
head = next;
if(next == null)
tail = null;
else
next.prev = null;
size--;
return value;
}
//맨 뒷단의 노드 삭제
private int unlinkLast() {
int value = tail.value;
Node prev = tail.prev;
tail = prev;
if(prev == null)
head = null;
else
prev.next = null;
size--;
return value;
}
private Node node(int index) {
if(index < (size >> 1)) {
Node x = head;
for (int i = 0; i < index; i++)
x = x.next;
return x;
}
else {
Node x = tail;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
//노드 삭제
private int unlink(Node x) {
if(x == head) {
return unlinkFirst();
}
else if(x == tail) {
return unlinkLast();
}
//중간 노드 삭제
int value = x.value;
x.prev.next = x.next;
x.next.prev = x.prev;
size--;
return value;
}
//succ 노드 앞에 노드 삽입
private void linkBefore(int value, Node succ) {
if(succ == head) {
linkFirst(value);
return;
}
Node newNode = new Node(succ.prev, value, succ);
succ.prev.next = newNode;
succ.prev = newNode;
size++;
}
@Override
public boolean add(int value) {
linkLast(value);
return true;
}
@Override
public void add(int index, int value) {
if(index == size) {
add(value);
return;
}
rangeCheck(index);
linkBefore(value, node(index));
}
@Override
public int remove(int index) {
rangeCheck(index);
return unlink(node(index));
}
@Override
public boolean remove(Integer value) {
int index = indexOf(value);
if(index == -1) return false;
unlink(node(index));
return true;
}
@Override
public int get(int index) {
rangeCheck(index);
return node(index).value;
}
@Override
public void set(int index, int value) {
rangeCheck(index);
node(index).value = value;
}
@Override
public boolean contains(int value) {
return indexOf(value) != -1;
}
@Override
public int indexOf(int value) {
Node cur = head;
for(int i=0; i<size; i++) {
if(cur.value == value)
return i;
cur = cur.next;
}
return -1;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return (size == 0);
}
@Override
public void clear() {
head = null;
tail = null;
size = 0;
}
public void print(){
System.out.println("--------");
Node node = head;
for(int i=0; i<size; i++){
System.out.println(node.value + " ");
node = node.next;
}
System.out.println("--------");
System.out.println();
}
}원형 연결 리스트 구현
원형 연결 리스트의 경우 link 연산과 unlink 연산이 한 가지 경우 밖에 없다. 중간에 노드 삽입, 삭제하는 경우다. 연결 리스트가 원형 구조이기에 앞단, 뒷단에 노드를 삽입하고 삭제하는 개념이 없다. 그래서 구현이 더 쉬워진다.
'Computer Science > DataStructure' 카테고리의 다른 글
| Binary Search Tree (0) | 2023.09.11 |
|---|---|
| Tree (0) | 2023.09.06 |
| ArrayList (0) | 2023.08.12 |
| Disjoint Set (분리 집합) (0) | 2023.03.03 |
| Graph (0) | 2022.10.27 |
